今回は、ひし形(というか任意の4点からなる四角形)と、ある点の衝突判定を行いたいと思います。
判定処理の概要ですが、以下図の通り任意の4点 A ~ D をそれぞれを線で結び四角形とし、そこに点 P を与え、それぞれ四角形の内(=衝突している)外(=衝突していない)という判定を行います。

この場合 P1 は「中」、P2 は「外」の判定になります。
但し、下図のように四角形の内角のいずれかが180°を超えている場合この処理は適用できません。

考え方
考え方は、四角形の4辺それぞれの辺ごとと、判定対象の点の位置関係を外積を用いて計算し、全ての辺の右側に点があれば「内側」、1つでも左側にあれば「外側」という判断を行います。
ある1辺の計算式を見ていきます。条件は以下の通りです。簡単のため、Y方向が同じ縦の辺を考えます。
- 点A(12, 10)
- 点B(12, 30)
- 辺AB→
- P1(7, 23)
- P2(18, 19)

この時結果の期待値は、P1 は辺の左、P2 は辺の右側となります。
外積の計算方法は右の通りです。|v1||v2|sin(θ) = x1y2-x2y1 = v1×v2
P1とAB→の関係はAB→とAP1→の2つの辺を作って外積の計算を行います。従って、AB→は(12 - 12, 30 - 10)=(0, 20)となり、AP1→は(12 - 7, 10 - 23)=(5, 16)、外積をとると、0 * 16 - 5 * 20 = -100となります。「マイナスなので左」と判断します。
P2とAB→の関係は上記と同様に、AB→とAP2→の外積となります。AB→(0, 20)、AP2→(-6, 9)=180、すなわち「プラスなので右」と判断します。
コード例
以下C#での実装例です。(VisualStudio2017 + C#7.0で作成しています)
まず、XYの組み合わせを持つ汎用データ構造、Point2f を用意します。
// 単純な2点の情報を表すクラス public class Point2f { public float X { get; private set; } public float Y { get; private set; } public Point2f(float x, float y) { this.X = x; this.Y = y; } public override string ToString() => $"({this.X}, {this.Y})"; }
次に、処理本体です。4つの点abcdと、判定対象のpを受け取って内側か外側かをboolで返すIsInSquareメソッドを用意します。戻り値は、内側の場合 true、外側の場合 false です。
// 衝突判定系の汎用処理クラス public static class CollisionUtil { // 指定した4点の中にpがあるかどうかを判定する // 但し、4つそれぞれの内角のいずれかが180度以上の場合、正しく判定できない。 public static bool IsInSquare(Point2f pa, Point2f pb, Point2f pc, Point2f pd, Point2f p) { float a = CalcExteriorProduct(pa, pb, p); float b = CalcExteriorProduct(pb, pc, p); float c = CalcExteriorProduct(pc, pd, p); float d = CalcExteriorProduct(pd, pa, p); Trace.WriteLine($"{a}, {b}, {c}, {d}"); bool res = a > 0 && b > 0 && c > 0 && d > 0; return res; } // 指定した2点間と1点の外積を計算する public static float CalcExteriorProduct(Point2f a, Point2f b, Point2f p) { // 点 a,b のベクトル var vecab = new Point2f(a.X - b.X, a.Y - b.Y); // ここは固定なら最初から計算しておくのもアリかも // 点a と 点のベクトル var vecpa = new Point2f(a.X - p.X, a.Y - p.Y); // 外積を計算する float ext = vecab.X * vecpa.Y - vecpa.X * vecab.Y; return ext; } }
で、上記メソッドを呼び出す側の処理です。
public static void Main(string[] args) { A=, B=, C=, D= & P== true Point2f pa = new Point2f(162, 212); Point2f pb = new Point2f(210, 112); Point2f pc = new Point2f(386, 152); Point2f pd = new Point2f(355, 244); Point2f pp = new Point2f(251, 179); // 結果を受け取る bool result = CollisionUtil.IsInSquare(pa, pb, pc, pd, pp); }
C#で確認プログラムを作成しました
C#とWPFで、上記の処理の動作確認用のプログラムを作成しました。
起動後に枠内を4回クリックすると、点を配置でき四角形を作成できます。Canvasに描画しているので座標系は左上が原点で右下に行くほど増加する系となっています。
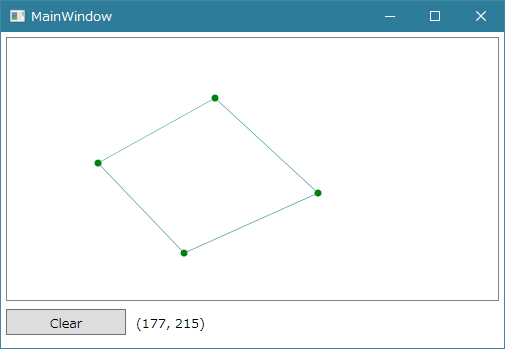
5回目以降のクリックで赤い点が一つ配置され、その点が四角形の中か外かを判定します。結果は画面下部のテキストに表示され、以下は画像では内側の判定となり、テキストにtrueと表示されています。

以下画像では外側判定となりテキストにfalseと表示されています。

上記確認プログラムを、GitHubにアップしました。VS2017でC#7.0以降であればダウンロード(もしくはClone)後にすぐにコンパイル・実行できると思います。良かったらコードだけでも確認してみてください。